DOCCOURSE PRAGUE 2005

Programme for pre-doctoral and doctoral students in

Modern Methods in Ramsey Theory

Prague, January 5 - March 31, 2005

Supported by the EU network COMBSTRU and by DIMATIA Prague.

LECTURES

January 24 - February 25, 2005

Lectures (Monday and Tuesday, 9-12):
Weeks 1-2: Ehud Friedgut, Jerusalem

Monday, Jan 24: Ramsey thm., Happy ending thm. (Erdos-Szekeres' and Tarsi's proofs), van der Waerden thm.. Hales-Jewett thm, Gallai thm.,
Tuesday, Jan 25: Roth's thm.
Monday, Jan 31: Description of Furstenberg's approach - proof of van der Waerden thm. using topology and algebra
Tuesday, Feb 1: Continuation of lectures - proof of Hindman's thm

Week 3: Vojtech Rodl, Emory, Atlanta

Monday, Feb 7: Discussion of Szemeredi's Regularity Lemma, its proof and limitations. Proof of the Theorem of Rusza and Szemeredi. Another proof of Roth's Theorem.
Tuesday, Feb 8: Proof of the Counting Lemma and discussion of its extensions. Solymosi's proof of the Ajtai-Szemeredi Theorem.

Weeks 4-5: Mathias Schacht, Humboldt University, Berlin

Monday, Feb 14: The Counting Lemma. Discussion of the Burr-Erdos Conjecture. Blow Up Lemma.
Tuesday, Feb 15: Hypergraph Removal Lemma and its connection to Szemeredi's Theorem. Discussion of straightforward extensions of the Regularity Lemma to hypergraphs and its limitations in view of the Removal Lemma. Discussion of a more refined approach to hypergraph regularity with a Counting Lemma. Lectures will be held in S7 (from 9 to 10:30) and S6 (from 10:40 to 12)
Monday, Feb 21: We continue with the proof of the removal lemma for K₄⁽³⁾, which implies r₄(n)=o(n). For that we
- discuss of the hypergraph regularity lemma and its proof
- prove the so-called dense counting lemma. This lemma is one of the important components in the proof of the appropiate counting lemma . Tuesday lecture will be held at Keiserstein Palace, Malostranske Namesti 23/37
Tuesday, Feb 22: We reduce the proof of the counting lemma to the dense counting lemma, which completes the proof of r₄(n)=o(n).
If time allows we discuss the extensions for general k.

Supervision for excercise solving (Monday and Tuesday, 14-17):
Mathias Schacht and Zdenek Dvorak

All lectures are held in S5 (2nd floor) unless noted otherwise.

Special lectures related to the DOCCOURSE:

Schedule in pdf, booklet: 1st week, 2nd week, 3rd week, 4th week, 5th week (including abstracts).

Wednesday, Feb 23

55th Mathematical Colloquium

Miklos Simonovits,Turan Problems, Ramsey Problems, Simple and Random-looking Extremal Structures

Abstract:: Turan and Ramsey type problems were always very closely related to each other.
For the original questions (i.e., Ramsey numbers and Turan numbers for complete graphs) the extremal graphs were simple looking for Turan type problems and very involved for the Ramsey case. When the selected excluded substructures were extended, the situation changed: Turan type problems with fuzzy extremal graphs and Ramsey extremal graphs with very regular, simple structures occurred.
In my talk I will analyse this strong relation through some specific examples. Among others, I will put emphasis on two basic cases, one of which is the problem of 3-coloring the edges of a complete graph and looking for monochromatic odd cycles:
Recently Skokan, Kohayakawa and myself improved the corresponding asymptotic result of Luczak, proving an old conjecture of Bondy and Erdos, at least for n large:
We have proved that if n>n₀ and K_4n-3 is 3-colored then it contains a monochromatic C_n (which is sharp for odd values of n. Some related results of Figaj, Luczak, Gyarfas, Ruszinko, G. Sarkozy, and Szemeredi will also be discussed.
The proof was obtained using the Regularity Lemma and the stability method. As I mentioned, the particular results will be embedded into discussing phenomena from the general setting.

Thursday, Feb 24

Vera T. Sos, Renyi Institute, Budapest, A Hierarchy of Randomness for Graphs

Abstract:: We formulate four families of problem with which we aim at distinguishing different levels of randomness.
The first one is completely non-random, being the ordinary Ramsey-Turan problem and in the subsequent three problems we formulate some randomized variations of it. These four levels form a hierarchy, the main topic of this work.
We formulate very briefly (and informally) the four questions for a special case. The questions are as follows:
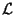Fix a family of graphs $\cal L$ and an integer r => 2.; (DD) How many edges guarantee for a graph G_n that if we r-color its edges arbitrarily, we always find a monochromatic L $\in$ $\cal L$ ?; (DR) How many edges guarantee for a graph G_n that in almost all r-edge-colorings, we find a monochromatic L $\in$ $\cal L$ ?; (RD) How many edges guarantee for a random graph R_n almost surely,that $r$-coloring its edges arbitrarily, we always find a monochromatic L $\in$ $\cal L$ ?; (RR) How many edges guarantee for a random graph R_n almost surely, that r-coloring its edges at random, almost all the r-colorings contain a monochromatic L $\in$ $\cal L$ ?

Friday, Feb 25

Miklos Ruszinko,Three-color Ramsey numbers for paths

Abstract:: For graphs G₁, G₂,..., G_r, the Ramsey number R(G₁, G₂,..., G_r) is the smallest positive integer n such that if the edges of a complete graph K_n are partitioned into r disjoint color classes giving r graphs H₁, H₂,..., H_r, then at least one H_i (1 $\le$ i $\le$ r) has a subgraph isomorphic to G_i. The existence of such a positive integer is guaranteed by Ramsey's classical result. The number R(G₁, G₂,..., G_r) is called the Ramsey number for the graphs G₁, G₂,..., G_r. There si very little known about the case when each G_i is a path P_n on n vertices. For r = 2 a well-known theorem of Gerencsér and Gyárfás states that

R(P_n, P_n) = $\displaystyle \Bigl\lfloor$ $\displaystyle {3n-2 \over 2}$ $\displaystyle \Bigr\rfloor$ .
For r $\ge$ 3 the Ramsey numbers for P_n are not known. We proof - for sufficiently large n - the following conjecture of Faudree and Schelp.

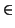
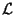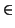
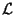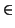
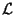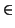
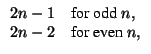
R(P_n, P_n, P_n) = $\displaystyle \left\{\vphantom{ \begin{array}{ll} 2n - 1 & \mbox{for odd}~n, \\ 2n - 2 & \mbox{for even}~n, \end{array}}\right.$ $\displaystyle \begin{array}{ll} 2n - 1 & \mbox{for odd}~n, \\ 2n - 2 & \mbox{for even}~n, \end{array}$
for the three-color Ramsey numbers for paths on n vertices. In an earlier version of this paper we proved the asymptotic result R(P_n, P_n, P_n) = (2 + o(1))n. This was also obtained independently by Figaj and Luczak. In the proof of the asymptotic result the main tools were the Regularity lemma and the following lemma, suggested by Luczak.
Lemma 1. For every $\eta$ > 0 there exists n₀ and $\varepsilon$ > 0 such that for n $\ge$ n₀ the following holds. For every 3-edge coloring of a graph G with n vertices and more than (1 - $\varepsilon$ )n $\choose2$ edges there exists a monochromatic connected matching covering at least (1 - $\eta$ )n/2 vertices of G.
To obtain the exact result we sharpen Lemma 1. This is a joint result of András Gyárfás, Gábor Sárközy, Endre Szemerédi and myself.
Abstract in postscript

COURSE: Modern Methods in Ramsey Theory

Ehud Friedgut (Jerusalem)

Vojtech Rodl (Emory, Atlanta)

Mathias Schacht (Humboldt University, Berlin)

Abstract:

Ramsey theory is a rich and thriving branch of combinatorics, originating in the late 20's and 30's in work of Ramsey and, independently, Erdos and Szekeres.

Roughly one can divide the approaches to Ramsey Theory into four main parts:

Straightforward combinatorial approaches.
Fourier analysis.
Ergodic theory: topological and algebraic methods.
Use of Szemeredi's Regularity Lemma and its extensions.

In this course we will give a brief taste of the first two methods and concentrate on the last two. This will include an introduction to two very different approaches that were developed in the late 70's and are still evolving and bearing fruit: on one hand the celebrated Szemeredi Regularity Lemma, one of the deepest and most influential results in combinatorics, and on the other hand methods developed by Furstenberg who shook the mathematical community by demonstrating how Ergodic Theory can yield deep combinatorial results.

Background: It is desirable that the students attending the course have some background in combinatorics, (e.g. basic graph theory), and a first course in topology (e.g. being familiar with the notion of compactness.)

Bibliography:

Ramsey Theory/ Graham, Rothschild and Spencer.
Recurrence in Ergodic Theory and Combinatorial Number Theory/ Furstenberg
Graph Theory [Chapters 7 and 9]/ Diestel
The Regularity Lemma and its Applications in Graph Theory/ Komlos, Shokoufandeh, Simonovits, Szemeredi, Theoretical Aspects of Computer Science (Tehran, 2000), Lecture Notes in Computer Science, vol. 2292, Springer, Berlin, 2002, pp. 84-112 (available on Simonovits webpage).
Extremal Problems on Set Systems / Frankl, Rodl, Random Structures and Algorithms 20 (2002) no. 2, 322-337

The course will begin by discussing the basic concepts of Ramsey theory, both finite and infinite. The course will be accompanied by additional lectures on related topics by other people present in Prague.

Call for applications

DIMATIA Centre at the Charles University Prague offers a three month study programme for PhD students and students preparing to enter a PhD programme in areas: Combinatorics and Graph Theory; Discrete and Computational Geometry; Combinatorial Optimization; Discrete Structures.

Information about the previous year's DOCCOURSE, which had 25 participants and which we believe was quite successful, can be found here.

The scientific programme in 2005 is focussed mainly on modern Ramsey Theory. It includes a five-week research-oriented course (speakers include E. Friedgut, V. Rodl and M. Schacht; see below for details), complemented by additional lectures on related subjects.

The contact persons and the leaders of the programme are J. Matousek (Charles University, Prague, matousek [at] kam.mff.cuni.cz) and J. Nesetril (Charles University, Prague, nesetril [at] kam.mff.cuni.cz).

A limited number of scholarships of approximately EUR 1000/month are available for students with a diploma or master degree in a field related to the topics of the programme (mathematics, computer science). Advanced diploma or master students can be considered as well if a feasible arrangement with their home institutions can be made. Students wishing to participate in the programme using other financial resources are also encouraged to apply; the acceptance will be limited by the capacity of the courses.

The accepted students are expected to participate in all of the programme.

Pre-doctoral students may prepare a PhD. research proposal during the programme, and after the programme there is a possibility of applying for a PhD. scholarship at one of the institutions of the COMBSTRU network.

The language of the programme is English. The programme is open to applicants of all nationalities but the support is restricted by EU regulations to citizens of the EU (except for the Czech Republic) and of countries associated to Framework 5 Programme (e.g., Bulgaria, Iceland, Israel, Liechtenstein, Norway, Romania, and Switzerland; the rules are complicated and developing - if in doubt, please check here or write to the organizers).

Applications with curriculum vitae, copies of certificates, thesis, areas of interest, and a letter of recommendation from the thesis advisor should be sent

either electronically (preferable), in an open format (Postscript, PDF), to

"matousek" at the domain "kam.mff.cuni.cz",
or by mail to

DOCCOURSE
Jiri Matousek
Department of Applied Mathematics
Malostranske nam. 25
118 00 Praha 1
Czech Republic

Application deadline is October 20, 2004. Applicants are notified of results by October 31, 2004.